-
Our Products
Our FundsFocus Funds
-
Self Care
Self-ServiceFind InformationWays To TransactPartner Solutions
-
Downloads
- Learnings
- About Us
-
More
-
Shareholders
-
Shareholders
-
Updates
-
-
SIP Calculators
- Back
-
Shareholders
Making sense of duration in debt funds

Jul 14, 2023
2 Mins Read
Listen to Article
It is common for debt market investors to dwell in detail on yields, interest rates and bond prices. But for money managers and investors, one critical aspect of debt funds is to reconcile all these factors for taking suitable decisions on buying the right bonds to suit their requirements. And that comes through the duration aspect of debt funds. We hear debt fund managers speak about ‘duration play’ to ride an interest rate cycle.
In short, duration in bond parlance measures how sensitive a debt security or portfolio is to interest rate moves.
Therefore, studying of duration in bonds becomes important to minimise losses and decide the best course of action during times of high Central Bank actions.
Before getting into duration, a quick take on some key relationships in the bond markets.
(Source: https://in.investing.com/rates-bonds/india-10-year-bond-yield-historical-data)
The first concept to note is the Macaulay Duration. By definition, it is the weighted average time period to maturity of a bond’s cash flows. Put simply, it is the time required by an investor to recover the bond’s price vis its cash flows – interest payouts.
We see that the Macaulay duration in this case is 7.61 years. Therefore, it would take 7.61 years for the bond holder to get back the bond’s price via its cash flows, or interest payouts.
Now, with the Macaulay Duration, we know the time to recover the bond price. But understanding the sensitivity of bond prices to rate movements is more important.
That’s where the modified duration comes in. It measures the movement in bond price for a percentage increase in interest rate. Therefore, for every 1% increase in interest rate, the bond price will fall by 6.48%. And for a 1% fall in interest rate, the bond price will increase by 6.48%.
The information herein is meant only for general reading purposes and the views being expressed only constitute opinions and therefore cannot be considered as guidelines, recommendations or as a professional guide for the readers. The document has been prepared on the basis of publicly available information, internally developed data and other sources believed to be reliable. The sponsor, the Investment Manager, the Trustee or any of their directors, employees, affiliates or representatives (“entities & their affiliates”) do not assume any responsibility for, or warrant the accuracy, completeness, adequacy and reliability of such information. Recipients of this information are advised to rely on their own analysis, interpretations & investigations. Readers are also advised to seek independent professional advice in order to arrive at an informed investment decision. Entities & their affiliates including persons involved in the preparation or issuance of this material shall not be liable in any way for any direct, indirect, special, incidental, consequential, punitive or exemplary damages, including on account of lost profits arising from the information contained in this material. Recipient alone shall be fully responsible for any decision taken on the basis of this document. Mutual Fund investments are subject to market risks, read all scheme related documents carefully.
This ability becomes critical because from late 2021 when inflation spiked globally and Central Banks around the world responded with interest rate hikes from early to mid-2022 and still continue to be on a tightening spree, although a few such as the US and India have paused for the time being.
The sudden rise in interest rates of anywhere from 250 basis points in the case of India and 500 basis points in the case of the US had the bond markets roiled, with yields spiking sharply.
We will look at the two popular metrics – Macaulay duration and Modified duration – to study the impact of interest rates on bond prices and the fund’s Net Asset Value (NAV).
Duration, interest rates and bond prices
Bond prices and yields move in opposite directions as they are inversely related. Bond prices fall when yields rise and vice versa. Interest rates and bond prices are also inversely related. But interest rates and yields are directly related. So, yields spike when interest rates are increased, and therefore bond prices fall. Thus, interest rate movements become important for debt security holders.
For example, the 10-year g-sec’s yield increased from 6.45% by December 31, 2021, to 7.61% by June 16, 2022, even as the RBI started increasing interest rates from May 2022.
The general formula for Macaulay Duration is = Face value of a bond/Annual interest paid
But a more detailed formula used to evaluate modified duration incorporates the present value (PV) and future value (FV) of cash flows.
So, Modified duration would be =
(PV of future annual interest payouts)/ (PV of time weighted interest payout)
For example, let’s say, a bond of Rs 1,000 is issued with a coupon of 7% and with a maturity profile of 10 years. The discount rate is assumed to be the inflation rate of around 6%.
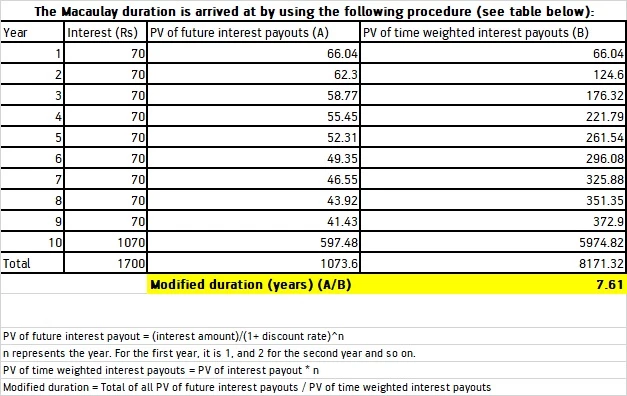

This is for one security. This calculation can be extended for an entire portfolio of bonds to arrive at an overall Macaulay duration.
SEBI’s guidelines are applicable for fund managers while deciding on the securities, depending on the category.
The portfolio of Ultra Short Duration Funds must have a Macaulay duration of 3-6 months. A medium duration fund is expected to have between 3 and 4 years as Macaulay duration, while for a Long Duration fund, this must be greater than 7 years.
Modified duration for sensitivity measurement
Mathematically,
Modified duration = (Macaulay Duration)/ (1+YTM/f)
Where: YTM is the yield to maturity and f is the frequency of interest payout.
Assuming a Macaulay duration of 7 years, YTM of 8% and an annual interest payment mode, we can calculate modified duration as:
= 7/ (1+8%/1)
Which is 6.48 years.

As a result, a debt fund that follows a duration strategy will fluctuate based on the above factors.
In general, long duration funds will fall when rates rise, while ultra short, short, liquid and money market funds are less affected by rate hikes. The reverse will hold true when rates are cut.
Depending on the outlook for inflation, interest rates and so on, the fund manager can play the duration strategy by shuffling securities with the right modified duration so that returns are optimized.
You May Also Like
Loading...





 1800-270-7000
1800-270-7000